ReactJS Tutorial# 5 – React Flux and Redux
What is Flux? its the obvious question that comes to our mind when we hear this word. Flux is an application architecture style. This is used by Facebook internally when working with React. So now we know that React Flux is not a library, it’s just pattern that we should follow when building user interfaces, especially when we are using React. Long story short – it is a way of thinking.
And with that being said we should know that there is a lot of libraries out there that are built on the top of this pattern. We will take a closer look later in this article.
Tutorial Index
- ReactJS Tutorial# 1 – An Introduction
- ReactJS Tutorial# 2 – Components and Props
- ReactJS Tutorial# 3 – Component State and Lifecycle
- ReactJS Tutorial# 4 – Forms, Events, and Keys
- ReactJS Tutorial# 5 – React Flux and Redux
- ReactJS Tutorial# 6 – ReactJS Best Practices
- 51-important-reactjs-interview-questions
As we already said, Flux is the application architecture that Facebook uses for building client-side web applications. Its usage is good with React, since it complements React’s composable view components by utilizing a unidirectional data flow.
When we are creating an application with Flux we have three major parts: the dispatcher, the stores, and the views (usually it is React components). This should not be confused with the Model-View-Controller (MVC) pattern. Because Flux eschews MVC in favor of a unidirectional data flow.
Structure and Data Flow
The Flux favor unidirectional data flow which means that data flows in a single direction. The diagram below should be the main mental model for every Flux programmer.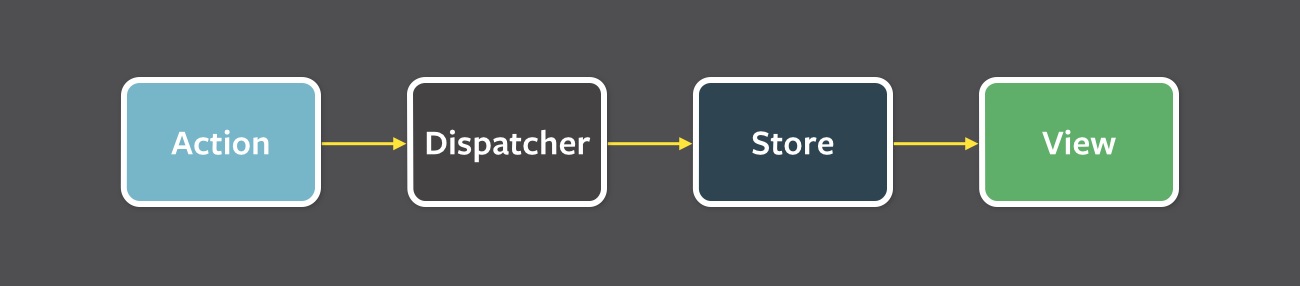
The major parts (dispatcher, stores, and views) are independent nodes with distinct inputs and outputs. The actions are just simple objects containing the new data and an identifying type property.
The views may init a new action to be propagated through the system in response to user interactions: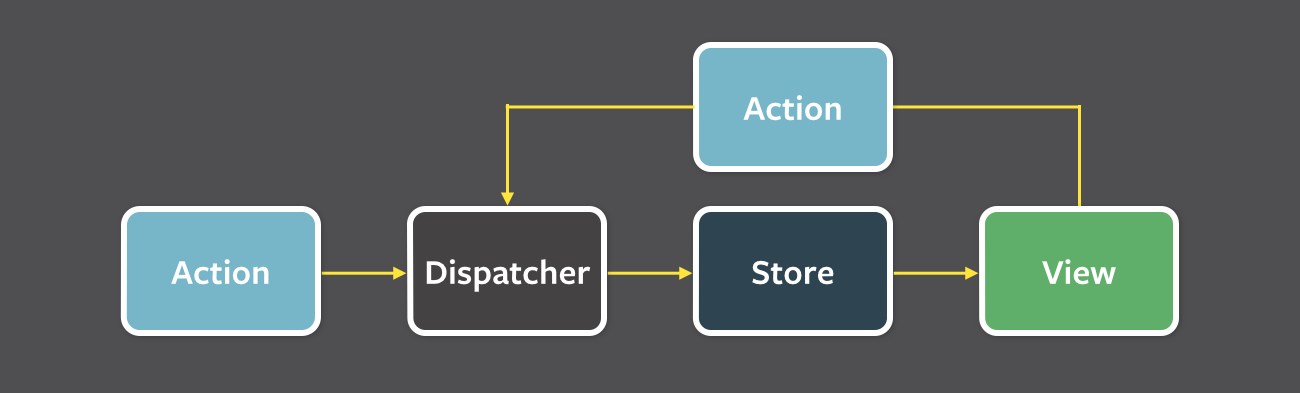
Ok ok. I know that it could be confusing at the beginning. Let’s go slowly and with an example.
First why this structure is good? Because it allows us to reason easily about our application in such a way that is reminiscent of functional reactive programming, or to be more precisely data-flow programming or flow-based programming, where data flows through the application in a single direction which means there are no two-way bindings. The second important thing here is that the application state is maintained only in the store (one of the major parts), allowing the different parts of the application to remain highly decoupled. And third… ok ok, let’s see an example.
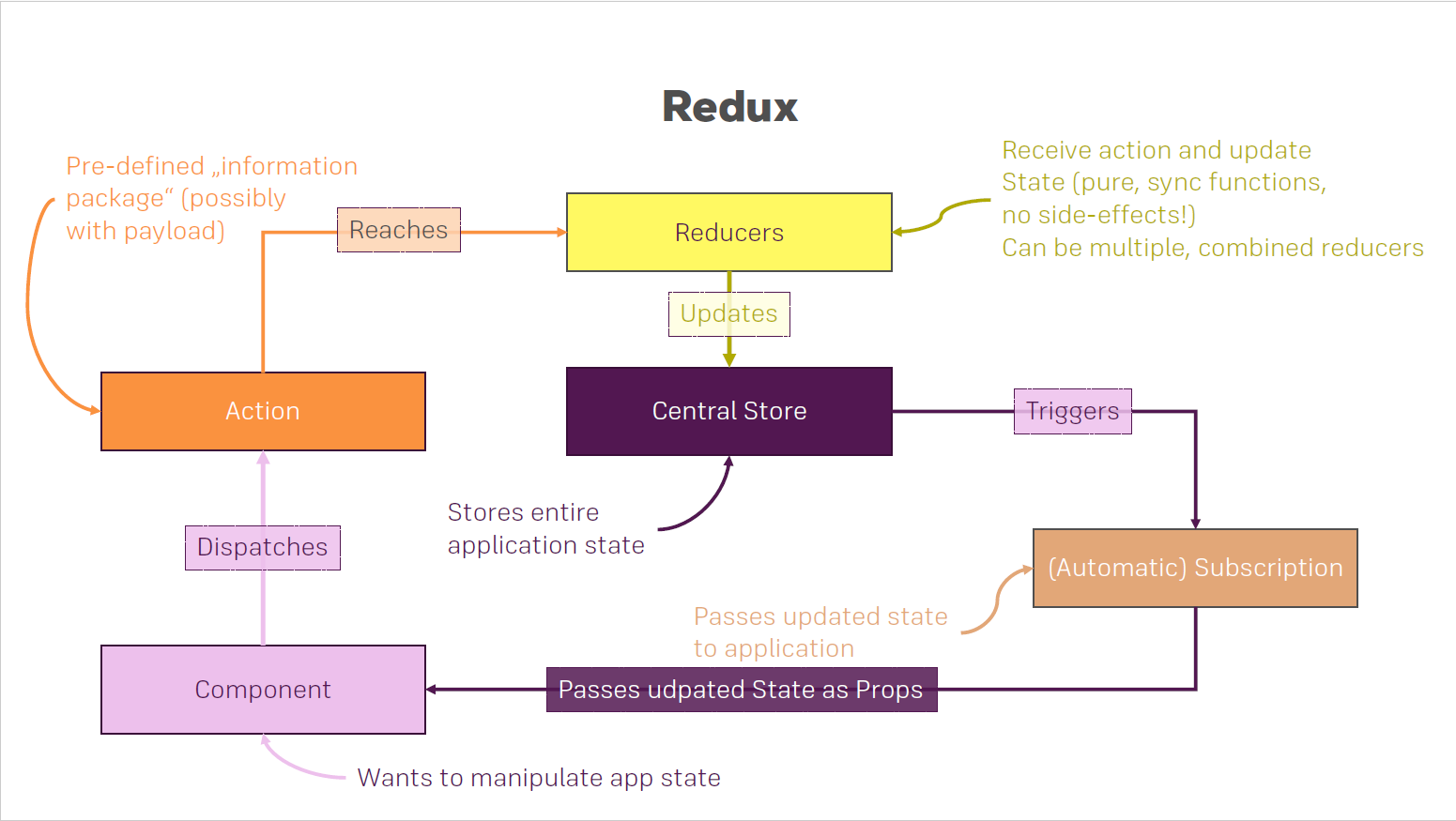
Redux
A new word? A new section? I guess you are confused with the first part and now something new. Let’s make it clear from the start. Flux is a pattern, as you already know. And Redux … is a library. Flux, to be honest, is nothing more than observer pattern modified a little so it will fit React. There are some small differences between this two, so let’s go through some of them.
In Flux it is a convention to have several stores per one application and each store is a singleton object. On the other hand, in Redux, the convention is to have a single store per application, and it is usually separated into data domains internally.
Redux doesn’t have dispatcher entity. Instead, the store has this option baked in. It exposes this function through its API so we can use it and not worry about anything.
According to Flux pattern, the logic of what to do on data that is received when some action is triggered is written in the store itself. In Redux this is done in the reducer function which is called on every action that gets dispatched, as we said, through the store API. It is important to notice here that in Redux, the store cannot be defined without a reducer function. Long story short, a Redux reducer is a simple function that as arguments receive the state and one action, and it returns the new state based on that action. In a Redux application, it is good practice to split your reducer into simpler functions. This is something that you would do with any other function. And do not forget – the smartest player in Redux is the reducer.
Before we show the example, let me show you one more image.
And now, let’s do some coding.
Reducer in Action
To show how Reducer work, we will create a small example. To achieve it run the following command:
|
1 |
npm init -y |
This will create a package.json file for us without asking any question.
As we already mentioned, Redux is a library so to use it we must first install it with help of npm. For this run :
|
1 |
npm install --save redux |
This will create a new folder called node_modules and a file package-lock.json on the same level where our package.json file is stored and in package.json will add the following text:
|
1 2 3 |
"dependencies": { "redux": "^4.0.1" } |
Now let’s create a JavaScript file where we will write our example. Create and open a new file- redux-example.js
Let’s start with the store. For that, we need to add something from Redux. Because we are going to run this file with the node, we should use node import syntax.
|
1 |
const redux = require('redux'); |
We should create another variable createStore which will refer to Redux createStore function. We will not execute it yet though.
|
1 |
const createStore = redux.createStore; |
Now let’s create our store.
|
1 |
const store = crateStore(); |
createStore like this will not do much though, because it needs a reducer to be passed as its argument. So before creating our store, we should create our reducer. And as we already know, the reducer is just a function with two parameters – state and action.
|
1 |
const rootReducer = (state, action) => { return state; } |
Our newly created reducer should pass into createStore. So the line above will now look like this.
|
1 |
const store = crateStore(rootReducer); |
We can see the current state of our store by calling function getState() on the store. Something like this:
|
1 |
console.log( store.getState() ); |
Right now, we will get undefined for our state value. To see that, execute our newly created example with the following command:
|
1 |
node redux-example.js |
Important: make sure you are inside the folder where the file is located.
To not get undefined at the start, we can set initial state for our state. SO before creating our reducer, create :
|
1 |
const initialState = { counter: 0 } |
and update the reducer like this
|
1 |
const rootReducer = (state = initialState, action) => { return state; } |
If we run node redux-example.js it again, in our terminal we will see: { counter: 0 }
We mentioned that we can update our store using an action which is dispatched from our store and handled by the reducer. It will look like this:
|
1 |
store.dispatch({type: 'INCREMENT'}); |
Notice that action is JavaScript object and it must have a property with key type and its value should be with capital letters. As a second argument to out action, we can set payload. So let’s create one more action and dispatch it.
|
1 |
store.dispatch({type: 'ADD', value: 10}); |
If we run the file again, what do you think the state of the store will be? Of course, you can go and run it, but before doing it I want you to think about what will be the state once you run it.
It will be still { counter: 0 } .
Why is that? Because we didn’t do any logic in our reducer for handling this actions.
Let’s do it.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
const rootReducer = (state = initialState, action) => { if(action.type === 'INCREMENT') { return { ...state, counter: state.counter + 1; } } if(action.type === 'ADD') { return { ...state, counter: state.counter + action.value } } return state; } |
In our reducer now we take the action, check what is its type and do the logic based on it. Notice that we return new JavaScript object where first we copy the old state with spread operator and then update that object.
So if we run the example now, we will get the following result.
{ counter: 0 }
{ counter: 11 }
This means that at the beginning our state is having the initialValue which is 0 for a counter after we dispatch two actions our state has a new value, which is 11.
Complete Code
The complete code for redux-example.js can be found below:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
const redux = require('redux'); const createStore = redux.createStore; const initialState = { counter: 0 } const rootReducer = (state = initialState, action) => { if(action.type === 'INCREMENT') { return { ...state, counter: state.counter + 1 } } if(action.type === 'ADD') { return { ...state, counter: state.counter + action.value } } return state; } const store = createStore(rootReducer); console.log(store.getState()); store.dispatch({type: 'INCREMENT'}); store.dispatch({type: 'ADD', value: 10}); console.log(store.getState()); |
Conclusion
We showed one short example where we manage to create store, reducer, and actions. These are the main parts of one application that is using Redux as its state manager. You can use Redux with React, but also and many other libraries. For React you will need to install Redux and React-redux. One more important thing to remember is – Store’s state cannot be mutable (or really, shouldn’t be). Remember it.
Hope you enjoyed the brief introduction on React Flux and Redux. Please feel free to let us know your views and comments.
Tutorial Index
- ReactJS Tutorial# 1 – An Introduction
- ReactJS Tutorial# 2 – Components and Props
- ReactJS Tutorial# 3 – Component State and Lifecycle
- ReactJS Tutorial# 4 – Forms, Events, and Keys
- ReactJS Tutorial# 5 – React Flux and Redux
- ReactJS Tutorial# 6 – ReactJS Best Practices
- 51-important-reactjs-interview-questions